Advances in RAD-seq phylogenetics¶
Deren Eaton
Phylogenetic methods are continually advancing, both in terms of the speed of analyses as well as in the statistical models that are applied. Increasingly, it is apparent that different phylogenomic regoins can yield heterogeneous signals that must be accomodated in our models, including variation in :
- base composition
- evolutionary rate
- topology
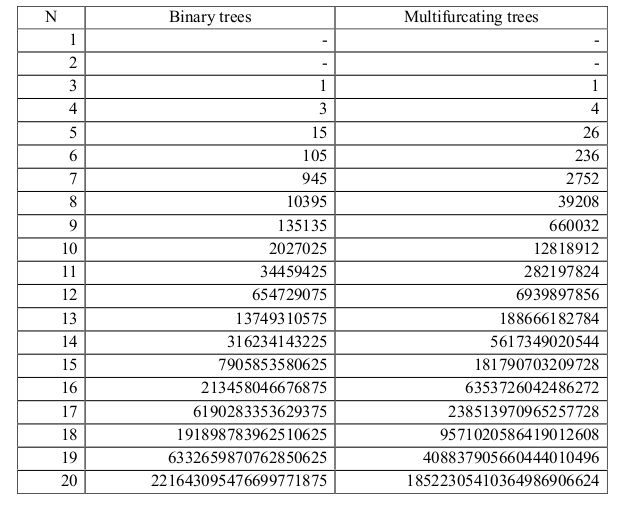
The big problem in phylogenetic inference: too many trees.¶
There are $(2n-3)!!$ possible rooted binary topologies to explain relationships among n samples. The size of tree space quickly becomes too large to search exhaustively.
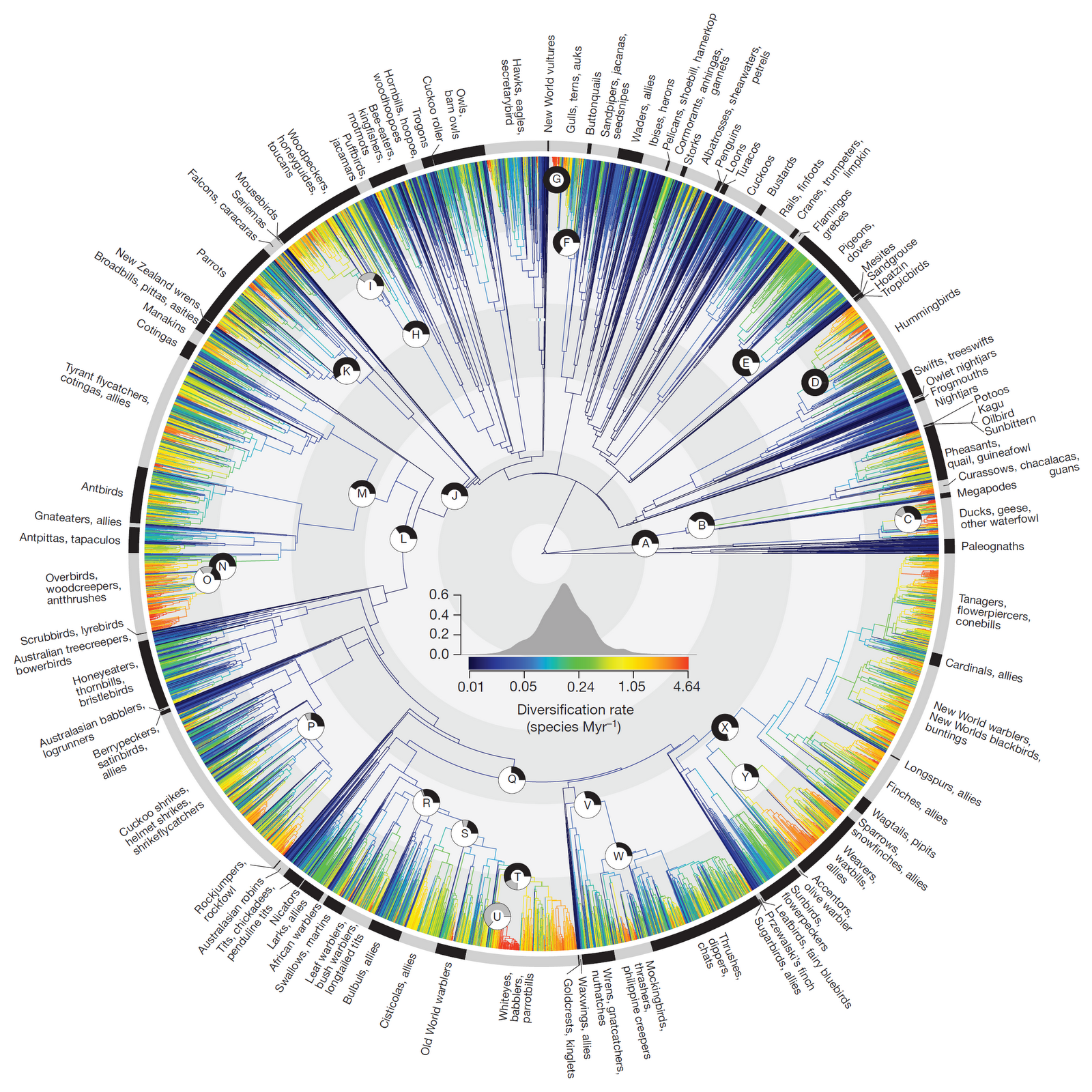
Large numbers of taxa¶
The first trees to include thousands of taxa were generated using mega-phylogeny approaches (Smith et al. 2008) which use data mining to assemble large supermatrices that contain few traditional markers (e.g., COI, cytB, ITS) sampled across many taxa. Recent examples include the large bird tree Jetz et al. 2012.
Likelihood calculation:¶
Maximum likelihood is the most commonly used statistical method for calculating the probability of a tree. In ML tree inference the goal is to optimize the likelihood of the data given a defined model $P(D|M)$, by estimating the parameters of the model. More complex models have more parameters to estimate.
The likelihood of the full tree is the product of the likelihood at each site. The more unique site patterns there are in an alignment, the longer the calculation takes.
Full genomes¶
Early phylogenomic studies typically compared few species (often model organisms) for which full genome data was available. The primary difficulties with using full genome data is in identifying proper phylogenetic markers. Many genomic regions are difficult to align, and it is difficult to identify homology between genes. For this reason, many studies with full genomes restrict phylogenetic analyses to the use of transcriptomes.
The influence of missing data¶
In large-scale megaphylogenies -- data mined matrices of few traditional markers across thousands of taxa -- missing data often ranges up to >90%.
In large-scale sub-genomic data sets, like RAD-seq, the proportion of missing data often ranges between 10-90%.
Importantly, the first type of problem is more sensitive to the problem of terraces in phylogenetic tree space Sanderson et al. 2012, where many taxa in the phylogeny share no information, whereas in the latter there is typically still significant phylogenetic information for all taxa.
Reduced-representation genome methods¶
Recently methods for subsampling the genome for phyogenomic methods have become popular. By sequencing a smaller proportion of the genome is it possible to more efficiently gather phylogenomic data from a larger number of samples. Regions are targeted either randomly (e.g., RAD-seq), generically (e.g., ultra-conserved elements), or specifically for a taxon (e.g., transcriptomes or targeted sequencing).
Comparisons¶
Number of loci:
- RAD > UCE > transcriptomes
Number of SNPs:
- RAD > UCE > transcriptomes
Informativeness of individual loci (gene trees):
- transcriptomes > UCE > RAD
Assembly difficulty/error:
- transcriptomes > UCE > RAD
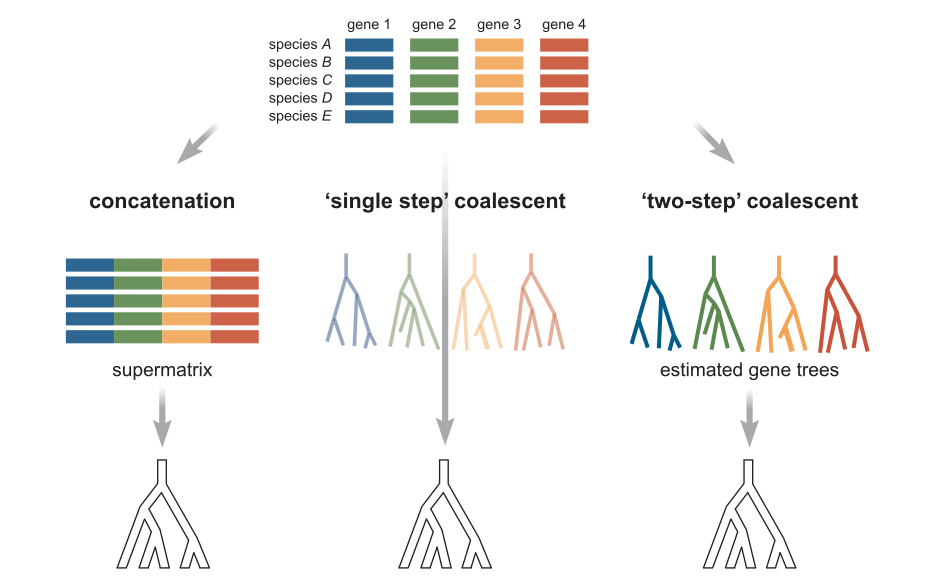
Concatenation methods¶
Concatenation continues to be the most popular method for phylogenetic inference. All data is analyzed simultaneously (although genes can be partitioned to be fit under different models). It is fast and mostly accurate. However, statistically inconsistent and can therefore give an incorrect topology when ILS is high, and it will consistently yield branch length errors (inflation) especially near the tips of the tree because it does not properly account for heterozygosity.
Species tree methods¶
It was recognized long ago that gene trees do not always match the species tree. This can be caused by many factors, including horizontal gene transfer, gene duplication, hybridization, and incomplete lineage sorting. Early methods to overcome this problem focused on minimizing deep coalescences (ILS) but newer methods now implement more advanced statistical models.
The multispecies coalescent¶
The coalescent is a mathematical model for the random joining of sampled gene lineages and they are followed back in time. The waiting time for coalescent events follows an exponential distribution, with a parameter that depends on the size of the underlying population. This gives a way of computing the probability associated with coalescent events within the branches of a species tree.
Ideally, gene trees are jointly estimated with the species tree. This is implemented in BEST, starBEAST, BPP, and other software. However, this method is very computation intensive and very slow. Limited to few taxa (~10).
Alternatively, two-step processes infer the gene trees first and then estimate a species tree afterwards by concordance among the gene trees. This is implemented in a variety of ways by software like ASTRAL, STAR, STEAC, BUCKy.
Phylogenetic invariants¶
This is an old method that has recently been revived to great popularity. It is a non-parametric method, meaning that it does not aim to infer parameters to fit a model. Instead, it uses a geometric model called the general Markov model. This is the basis of the SVDquartets method Chifman & Kubatko 2014 and tetrad (Eaton unpublished).
Theory resources:
- Cavender & Felsenstein (1987)
- Lake (1987)
- Eriksson (2008)
- Allman & Rhodes (2007)