Notebook 10.1: kmers & de Bruijn graphs¶
Reading:¶
This notebook is meant to accompany the following assigned article: Compeau, Phillip E. C., Pavel A. Pevzner, and Glenn Tesler. 2011. “How to Apply de Bruijn Graphs to Genome Assembly.” Nature Biotechnology 29 (11): 987–91. https://doi.org/10.1038/nbt.2023.
Learning objectives:¶
By the end of this notebook you should:
- Understand the concept of kmers.
- Be able to extract kmers from a string using Python.
kmers and the de Bruijn graph¶
kmers are substrings of length k of a larger string. The concept of kmers is used widely within computational genomics, both for mathematical reasons having to do with their application in graph theory, as well as for practical computational reasons having to do with the way they can be efficiently stored in memory and compared as a way of measuring similarity of genomic regions.
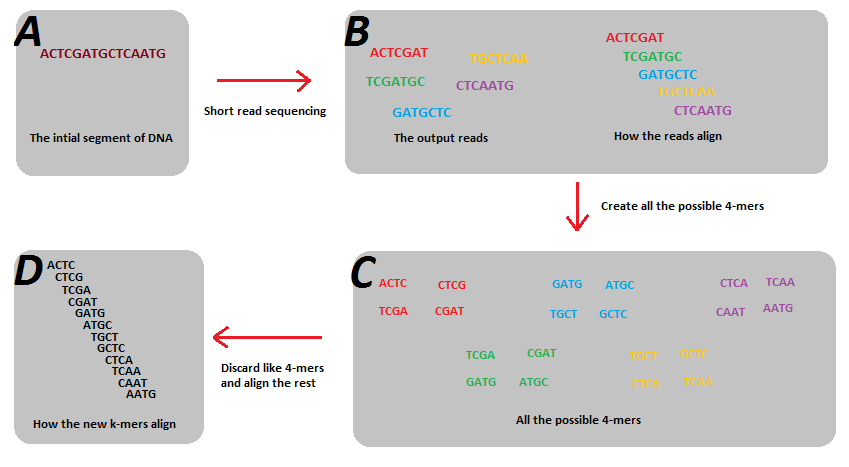
The de Bruijn graph is a mathematical construct used in genome assembly and other network based problems. It relies on the conjecture that a sequence can be reconstructed by substrings of that sequence if all substrings are present and overlap by n-1 (more on this later). An example type of substring is genomic short read sequences, which are a subset of the full genome sequence they are generated from. In practice, short reads may not overlap each other by n-1, but by using smaller kmers from each of many short reads more substrings can be generated which may more easily overlap by n-1 and thus be used to reconstruct the sequence. See image for example.
How many kmers are possible?¶
There exist n$^k$ k-mers in an alphabet containing n symbols: for example, given the DNA alphabet comprising A, T, G and C nucleotides, there are 4$^3$ = 64 trinucleotides (3mers). Similarly, your reading shows an example of a binary alphabet (0s and 1s) in which the number of 3mers is 2$^3$ = 8.
We can calculate this easily:
# number of nucleotides in DNA alphabet, e.g., ACGCGCGTATATTT
n = 4
# kmer size
k = 3
# n (number of items in alphabet) raised to k (size of kmer)
n ** k
# number of items in binary alphabet: e.g., 010101110000
n = 2
# kmer size
k = 3
# n (number of items in alphabet) raised to k (size of kmer)
n ** k
# number of nucleotides in DNA alphabet, e.g., ACGCGCGTATATTT
n = 4
# kmer size
k = 8
# n (number of items in alphabet) raised to k (size of kmer)
n ** k
How many kmers are in a sequence¶
A given sequence may be composed of all possible kmers in its alphabet, or by only a subset of kmers that are possible. Since kmers are just subsets of a larger string we can use slicing to select kmers from strings in Python. Above we saw that there are 64 possible 3mers in the DNA alphabet. The small genome below contains only 10 kmers.
# define a small genome string
genome = "ATGGCGTGCA"
# define the kmer length
k = 3
# iterate over starting positions of the genome string
for start_position in range(len(genome)):
# get 3-mer by slicing start position to start position + 3
kmer = genome[start_position: start_position + k]
# if the kmer is at the end then wrap-around to beginning
klen = len(kmer)
if klen < k:
kmer += genome[0: k - klen]
# print the kmer
print(kmer)
Hamiltonian and Eulerian cycles/paths¶
Your reading provides an example of the contig sequence "ATGGCGTCGCA" that is covered by three short read sequences (shown below), each of which partially overlaps the full contig sequence. We can see visually that any individual read does not contain enough information to construct the full contig, but that in combination the three reads could. The trick of genome assembly is figuring out the correct positioning and ordering of reads such that they will overlap correctly to represent the full genome sequence. Through the development of graph theory this problem can be re-stated by assigning the kmers in a string as nodes or edges in a graph and finding the shortest cycle/path that visits each node once (the Eulerian cycle).
genome = "ATGGCGTGCA"
read1 = "CGTGCAA"
read2 = "ATGGCGT"
read3 = "CAATGGC"
For the purpose of genome assembly it is convenient to split up these reads into smaller kmers so that there are more individual bits that can cover each part of the genome, and so that those bits can be tiled to overlap by n-1 positions. When the data are represented in this way it is easier to find a unique path -- a unique way in which to order the kmers that will reconstruct the genome string. Below I wrote out the 10 kmers in this string that we extracted computationally using slicing above.
genome = "ATGGCGTGCA"
kmer1 = "ATG"
kmer2 = "TGG"
kmer3 = "GGC"
kmer4 = "GCG"
kmer5 = "CGT"
kmer6 = "GTG"
kmer7 = "TGC"
kmer8 = "GCA"
kmer9 = "CA" + "A" # these wrap around to the beginning again
kmer10 = "A" + "AT"
One way to find the correct order of kmers is to construct a graph using pairwise alignments to connect kmers as nodes as in the graph. This is the basis for Hamiltonian genome assembly methods. An alternative approach is to represent the problem as a de Bruijn graph, where the kmers represent edges of the graph rather than the nodes.
As described in the paper the de Bruijn graph method does not require measuring pairwise differences between every pair of sequences whereas the Hamiltonian graph method does. For short-read data where we have many millions of reads this would be too time consuming. Instead, for de Bruijn graphs we only need to measure whether kmers match identically at the n-1 portion that they overlap. This calculation is very fast. In this graph the edges are the kmers and the nodes are the (k-1)mers.
# genome sequence for the exercise
genome = "AAAACCCCTTTTGGGGATATCGCGATATCGCG"
# write your function here
def get_kmers(sequence, k):
kmers = []
for i in range(0, len(sequence)):
kmer = sequence[i: i+k]
if len(kmer) == 5:
kmers.append(kmer)
return kmers
# execute your function on the genome here
get_kmers(genome, 5)